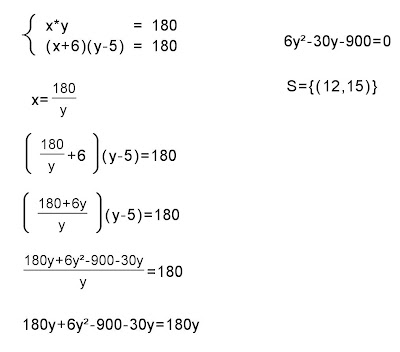skip to main |
skip to sidebar

* CONTRIBUIR PARA QUE A MATEMÁTICA SEJA ACESSÍVEL A TODOS DE MANEIRA PRAZEROSA. E QUE ESTA POSSA PROMOVER UMA EDUCAÇÃO MAIS EFICIENTE, TRANSFORMANDO A PESSOA EM CIDADÃO AUTÔNOMO E CONSCIENTE DE SEUS DIREITOS E DEVERES NO MUNDO.
Ampliação - Razão de semelhança
GeoGebra Planilha dinâmica
|
Prof. Joelson Lima, Criado com GeoGebra |
Teorema de Pitágoras
Teorema de Pitágoras - GeoGebra Planilha dinâmica
Teorema de Pitágoras
Prof. Joelson Lima, Criado com GeoGebra |
Demonstração geométrica 01 do teorema de Pitágoras - GeoGebra Planilha dinâmica
Demonstração geométrica 01 do teorema de Pitágoras
Prof. Joelson Lima, Criado com GeoGebra |
Demostração geométrica 02 do teorema de Pitágoras - GeoGebra Planilha dinâmica
Demostração geométrica do teorema de Pitágoras
Prof. Joelson Lima, Criado com GeoGebra |
quinta-feira, 16 de dezembro de 2010
Exercícios resolvidos sobre: Perímetro - Soma dos ângulos internos de um polígono - Ângulo central e inscrito - Sistema de equações do 1º grau
Exercícios resolvidos sobre: Relações métricas no triângulo retângulo - Teorema das cordas - Segmentos secantes e tangentes - Área de figuras
quarta-feira, 1 de dezembro de 2010
Sistema de equações do 2º grau
Problema:
* Um pintor gastou R$ 180,00 na compra de algumas latas de tinta em uma promoção, pagando com um desconto de R$ 5,00 por unidade. Esse desconto permitiu que ele comprasse exatamente seis latas a mais do que havia previsto. O preço de uma lata, sem desconto, é
R$ 15,00.
R$ 13,50.
R$ 12,00.
R$ 11,80.
R$ 10,50.
Solução:
Seja x o número de latas de tinta e y o preço sem desconto. De acordo com os dados do problema, montamos o sistema abaixo:
Como o preço é um valor positivo, temos que o preço sem desconto de cada lata de tinta é igual a R$ 15,00.
Com o preço sem desconto (R$ 15,00), compra-se 12 latas de tinta, com desconto (R$ 10,00), compra-se 18 latas (6 latas a mais).
Bom Estudo!
* Um pintor gastou R$ 180,00 na compra de algumas latas de tinta em uma promoção, pagando com um desconto de R$ 5,00 por unidade. Esse desconto permitiu que ele comprasse exatamente seis latas a mais do que havia previsto. O preço de uma lata, sem desconto, é
R$ 15,00.
R$ 13,50.
R$ 12,00.
R$ 11,80.
R$ 10,50.
Solução:
Seja x o número de latas de tinta e y o preço sem desconto. De acordo com os dados do problema, montamos o sistema abaixo:
Como o preço é um valor positivo, temos que o preço sem desconto de cada lata de tinta é igual a R$ 15,00.
Com o preço sem desconto (R$ 15,00), compra-se 12 latas de tinta, com desconto (R$ 10,00), compra-se 18 latas (6 latas a mais).
Bom Estudo!
terça-feira, 23 de novembro de 2010
sexta-feira, 19 de novembro de 2010
Área do retângulo e do semicírculo
05) Calcule o valor da medida da área hachurada na figura a seguir.
Solução:
Bom estudo!
Solução:
- A medida da área pintada é igual a medida da área do retângulo (base 8 cm e altura 4 cm) subtraindo-se a medida da área dos setores circulares;
- Observe que a medida da área dos dois setores circulares é igual a metade da medida da área do círculo de raio 4 cm;
Bom estudo!
quinta-feira, 18 de novembro de 2010
Área do semicírculo
04) Determine a área da região colorida.
Solução:
- A medida da área pintada é igual a medida do semicírculo maior, subtraindo-se a medida da área do semicírculo médio;
- Observe que a área pintada abaixo do diâmetro da circunferência é igual à parte não pintada acima do diâmetro (semicírculo menor);
Logo a medida da área pintada é igual a:
Bom estudo!
Área do triângulo equilátero e do semicírculo
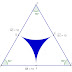
03) Determine a área da figura que está colorida.
Solução:
Solução:
- A área pintada é igual à medida da área do triângulo equilátero, subtraindo-se a medida da área dos 3 semicírculos;
- Para calcular a área do triângulo, precisamos da medida da base (8 cm) e da medida da altura (h);
Logo o valor da medida da área pintada é:
Bom estudo!
Área do triângulo equilátero e do círculo
02) Na figura, ABC é um triângulo equilátero de lado 10 cm; M, N e P são pontos médios dos lados AB, AC e BC, respectivamente. Calcule a área da região colorida.
Solução:
- A área pintada é igual a área do triângulo equilátero subtraindo-se a área dos setores circulares;
- juntando-se as áreas dos setores circulares, obtemos a metade da área do círculo de raio 5 cm;
- Para calcular a área do triângulo equilátero, precisamos do valor da medida da base (10 cm) e o valor da medida da altura (m);

Bom estudo!
quarta-feira, 17 de novembro de 2010
Área do quadrado e do círculo
01) Calcule a área colorida na figura.
Solução:
Bom estudo!
Solução:
- Observe que a área pintada (em azul), corresponde à área do quadrado de lado 8 cm subtraindo-se a área dos quatro setores circulares.
- Observe também que cada setor circular corresponde à quarta parte do círculo;
- Juntando-se os quatro setores temos um círculo completo de raio 4 cm;
Bom estudo!
quinta-feira, 21 de outubro de 2010
Espaço para dúvidas!
Olá pessoal!
Está aberto mais esse espaço para que você compartilhe ideias, dúvidas e questões com os colegas e com o professor.
Utilizem sem moderação!
Abraço a todos e bom estudo!
Está aberto mais esse espaço para que você compartilhe ideias, dúvidas e questões com os colegas e com o professor.
Utilizem sem moderação!
Abraço a todos e bom estudo!
Total de visualizações de página
Meu Perfil

- Joelson Lima da Silva
- JOÃO PESSOA, PARAÍBA, Brazil
- Graduado em Licenciatura Plena em Matemática pela UFPB em 2004; Especialização em Ensino da Matemática pela Universidade Estadual Vale do Acaraú em 2008
Postagens populares
-
Olá pessoal! Está aberto um espaço para tirar dúvidas relativas a unidade 2 (Geometria). Deixe aqui sua dúvida ou responda a dúvida do seu...
-
Olá pessoal! O teorema de Pitágoras é uma das relações entre os lados de um triângulo retângulo com mais aplicações na geometria. Existe...
-
Olá pessoal! Estamos de volta com os nossos estudos. Use esse espaço para discutir e tirar suas dúvidas com os colegas e com o professor....
-
02) Na figura, ABC é um triângulo equilátero de lado 10 cm; M, N e P são pontos médios dos lados AB, AC e BC, respectivamente. Calcule a áre...
Minha lista de blogs
-
-
Dialogo no ciberespaço : O que é uma Boa Aula em Matemática? - *Roberto Capistrano* É comum ouvir dos alunos referirem-se a seus professores com base nas formas e características de seu trabalho em sala de aula, como ...Há 9 anos
-
Nunca deixe de sonhar! - Iniciando mais um semestre letivo, esta é a minha mensagem para vocês: Nunca deixem de sonhar! Agora, vamos colocar no papel: Imagine que você está escreve...Há 10 anos
-
-
Falando um pouco sobre ângulo - This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.comHá 14 anos
-
Critérios de divisibilidade. - Alguns critérios e exercícios sobre divisidilidade Clik aqui ----> *CRITÉRIOS DE DIVISIBILIDADE.*Há 15 anos
-
Gabarito da Lista e da Revisão de Química - Boa noite pessoal, Estou aparecendo aqui aos 45 minutos do 2º tempo do Sábado, mas pelo menos aqui estão a lista e a revisão de química resolvidas e comenta...Há 15 anos
-
Como elaborar um projeto para construir um website. - Elaborar um WebSite requer organização e gestão de recursos. Antes de estabelecer um preço faça o planejamento a médio e longo prazo do seu projeto. Prepa...Há 15 anos
-
DICAS PARA RESOLUÇÕES DE QUESTÕES EM VESTIBULARES E CONCURSOS - Dica 1: Na leitura das questões muitos alunos começam a ler a questão e, sem terminar de ler todo o enunciado, acham que já sabem o que o problema está pe...Há 15 anos
-
-