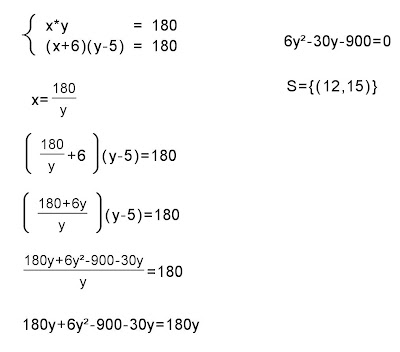Exercícios resolvidos sobre: Perímetro - Soma dos ângulos internos de um polígono - Ângulo central e inscrito - Sistema de equações do 1º grau

Exercícios resolvidos sobre: Relações métricas no triângulo retângulo - Teorema das cordas - Segmentos secantes e tangentes - Área de figuras

Sistema de equações do 2º grau

Problema:

* Um pintor gastou R$ 180,00 na compra de algumas latas de tinta em uma promoção, pagando com um desconto de R$ 5,00 por unidade. Esse desconto permitiu que ele comprasse exatamente seis latas a mais do que havia previsto. O preço de uma lata, sem desconto, é


R$ 15,00.

R$ 13,50.

R$ 12,00.
R$ 11,80.

R$ 10,50.


Solução:
 
Seja x o número de latas de tinta e y o preço sem desconto. De acordo com os dados do problema, montamos o sistema abaixo:
 

Como o preço é um valor positivo, temos que o preço sem desconto de cada lata de tinta é igual a R$ 15,00.

Com o preço sem desconto (R$ 15,00), compra-se 12 latas de tinta, com desconto (R$ 10,00), compra-se 18 latas (6 latas a mais).

Bom Estudo!

Recuperação 3º bimestre

Olá pessoal!

Segue os arquivos da recuperação do 3º bimestre.



Bom estudo!

Área do retângulo e do semicírculo

05) Calcule o valor da medida da área hachurada na figura a seguir.

Solução:

• A medida da área pintada é igual a medida da área do retângulo (base 8 cm e altura 4 cm) subtraindo-se a medida da área dos setores circulares;
• Observe que a medida da área dos dois setores circulares é igual a metade da medida da área do círculo de raio 4 cm;

Logo a medida da área hachurada é:

Bom estudo!

Área do semicírculo

04) Determine a área da região colorida.

Solução:

• A medida da área pintada é igual a medida do semicírculo maior, subtraindo-se a medida da área do semicírculo médio;
• Observe que a área pintada abaixo do diâmetro da circunferência é igual à parte não pintada acima do diâmetro (semicírculo menor);

Logo a medida da área pintada é igual a:

Bom estudo!

Área do triângulo equilátero e do semicírculo

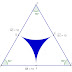
03) Determine a área da figura que está colorida.

Solução:

• A área pintada é igual à medida da área do triângulo equilátero, subtraindo-se a medida da área dos 3 semicírculos;
• Para calcular a área do triângulo, precisamos da medida da base (8 cm) e da medida da altura (h);

Logo o valor da medida da área pintada é:

Bom estudo!



Área do triângulo equilátero e do círculo

02) Na figura, ABC é um triângulo equilátero de lado 10 cm; M, N e P são pontos médios dos lados AB, AC e BC, respectivamente. Calcule a área da região colorida.

Solução:

• A área pintada é igual a área do triângulo equilátero subtraindo-se a área dos setores circulares;
• juntando-se as áreas dos setores circulares, obtemos a metade da área do círculo de raio 5 cm;

• Para calcular a área do triângulo equilátero, precisamos do valor da medida da base (10 cm) e o valor da medida da altura (m);
  
  
  

Portanto a área pintada é igual a:
 
 



Bom estudo!



Área do quadrado e do círculo

01) Calcule a área colorida na figura.

Solução:

• Observe que a área pintada (em azul), corresponde à área do quadrado de lado 8 cm subtraindo-se a área dos quatro setores circulares.
• Observe também que cada setor circular corresponde à quarta parte do círculo;
• Juntando-se os quatro setores temos um círculo completo de raio 4 cm;

Portanto a área pintada (em azul) é calculada da seguinte forma:

Bom estudo!

Espaço para dúvidas!

Olá pessoal!

Está aberto mais esse espaço para que você compartilhe ideias, dúvidas e questões com os colegas e com o professor.

Utilizem sem moderação!

Abraço a todos e bom estudo!

2ª prova 3º bimestre 2010

Olá pessoal!


Segue as provas resolvidas para material de estudo.


Bom estudo!

Prova - Nota qualitativa

Olá pessoal!

A correção da prova de recuperação da nota qualitativa do 2º bimestre.



Bom estudo!

Resolução da 1ª avaliação do 3º bimestre

Olá pessoal!

A resolução da primeira prova do terceiro bimestre sobre Álgebra (produtos notáveis - 8º ano) e Equação do segundo grau (9º ano), está disponível logo abaixo.



Bom estudo a todos!

Respostas

Olá pessoal!

Unidade 3: Álgebra I - Equação do 2º grau

Página 125
2) (gin+gin/7)+1/11(gin+gin/7) = 60 gin
3) F = x(x-1)
4)  a) 30;42  c) 21 d) x(x-1) = 420

Página 126
1) a) 5  b)8  c) 2  d) 4  e) 7/6  f) 1/3 g) √5  h) 11  i) 9  j) 1/8 k) 8  l) √6
Em foco
1) a)V  b) V  c) V  d) V  e) V f) F  g) V h) V  i)F  j)V  k)F
2)(x/3)(x/4) = 300
3)x²/12 = 300 => x²=3600=>x=60

Página 128

Descoberta
1)x²-5x=36
2)Sim
3) a)-4;6 b)-7;1  c)-13;5  d)√2-5 ;-√2-5 e) 2+√3;2- √3 f)-5/3; 3 g)-6;10 h)-5;-1 i)1+√5;1-√5 j)-7;-1
Em foco
1)30m
2)4√2
3)32cm
4)10cm
5)64m

Página 130
6) a)0;3 b)8;-2 c)0;3 d)-2;5 e)5 f)0;-5 g)1;5 h)-7;4 i)0;-3 j)-√2;-√3
7)6cm

Página 132
8)Base=5cm; Altura=8cm
9)x=5cm
10)3cm
11)54
12)7

Página 133
13)AB=6√3cm
14)a=√2
15)2cm

Página 134
16)3cm
Descoberta
2)2x²-4x=0
3)x=2

Página 135
6)Perímetro do quadrado=12√6cm ;Perímetro do retângulo=30cm
Oficina de...
2)27cm

Equação do 2º grau

Olá pessoal!

Este é mais um material de estudo interessante sobre equações do 2º grau. Sugestão da nossa colega Mônica - 9º ano.

Assista e estude bastante!

Fórum: Dúvidas sobre Monômios, produtos notáveis 8º ano

Olá pessoal!

Estamos de volta às nossas atividades. Vamos usar esse espaço para tirar dúvidas e compartilhar conhecimentos.

Revisão dia 26/08/2010



Bom estudo!

Fórum: Dúvidas sobre Equação do 2º grau 9º ano

Olá pessoal!


Estamos de volta com os nossos estudos. Use esse espaço para discutir e tirar suas dúvidas com os colegas e com o professor.

Revisão 26/08/2010



Bom estudo!

Trigonometria no triângulo retângulo

Olá pessoal!

O vídeo trata do conceito de trigonometria e das razões trigonométricas, seno, cosseno e tangente. Mostra também uma tabela de valores do seno, cosseno e tangente de alguns ângulos.


Bom estudo!

Fórum: Dúvidas sobre Olimpíada Brasileira de Matemática

Olá pessoal!

Coloque aqui suas dúvidas sobre as questões da OBM. Se houver alguma dúvida de seu colega que você saiba responder, coloque-a aqui no fórum.

Bom estudo!

Fórum: Dúvidas sobre o provão 2º bimestre 8º e 9º ano

Olá pessoal!

Coloque aqui nos comentários, sua dúvida sobre os conteúdos do provão. Caso você saiba responder a dúvida do seu colega, responda aqui no fórum.

Bom estudo a todos!

Conteúdo para o provão - 2º bimestre - Colégio Líder

Olá pessoal!

Segue o conteúdo do provão:

MATEMÁTICA 8º ANO



• Posições relativas entre duas retas:


o Paralelas;


o Concorrentes: Perpendiculares e inclinadas;


o Reversas;


o Coincidentes;


• Segmento:


o Conceito;


o Representação;


• Ângulos formados por retas paralelas cortadas por transversais;


• Ângulos internos de um triângulo;


• Ângulos internos de um quadrilátero;


• Postulados ou axiomas e teoremas:


o Hipótese e Tese;


o Demonstrações;



MATEMÁTICA 9º ANO



• Teorema de Pitágoras;


• Congruência e semelhança de figuras geométricas;


• Triângulos semelhantes;


• Teorema de Tales;


• Casos de semelhança nos triângulos:


o L.A.L.;


o L.L.L.;


o A.L.A.;


• Relações métricas no triângulo retângulo;


• Razões trigonométricas:


o Seno;


o Cosseno;


o Tangente;


Bom estudo!

1ª prova 2º bimestre resolvida

Olá pessoal!

Segue a resolução da 1ª prova 2º bimestre. Assuntos:

8º ano:

• Posições relativas entre retas;
• Segmento;
• Ângulos formados por retas paralelas cortadas por transversais;
• Teorema, demonstração;
• Translação, rotação;
• Simetria axial e pontual (central)

9º ano:

• Conceito de hipotenusa e catetos;
• Teorema de Pitágoras;
• Ampliação e redução de figuras;
• Triângulos semelhantes;
• Paralelas e transversais;
• Teorema de Tales;
• Casos de semelhança nos triângulos.

Bom estudo!

Revisão 8º e 9º ano para a 1ª prova 2º bimestre Líder

Olá pessoal!

Segue a revisão vista em sala de aula (20/05/10 e 21/05/10) sobre Geometria.
Assuntos abordados na revisão do 8º ano:

Unidade 2: Geometria

• Segmentos;
• Posições relativas entre retas;
• Retas paralelas cortadas por transversais;
• Ângulos colaterais (internos e externos);
• Ângulos correspondentes;
• Ângulos alternos (internos e externos);
• Demonstração;
• Simetria pontual e axial;
• Translação.

Assuntos abordados na revisão do 9º ano:

Unidade 2: Geometria

• Conceito de hipotenusa e catetos;
• O teorema de Pitágoras;
• Conceito de ampliação e redução de figuras;
• Conceito de congruência e semelhança em figuras geométricas;
• Triângulos semelhantes;
• Paralelas e transversais;
• Teorema de Tales;
• Casos de semelhança nos triângulos.

Abram o arquivo, vejam com calma e repita se sentir necessidade!

Coloque um comentário à respeito do assunto abordado!


Bons estudos!!!

Fórum: Dúvidas sobre Geometria 8º e 9º ano

Olá pessoal!

Está aberto um espaço para tirar dúvidas relativas a unidade 2 (Geometria). Deixe aqui sua dúvida ou responda a dúvida do seu colega sobre os conceitos estudados essa semana ou alguma questão que não conseguiu resolver. Ensinando também se aprende!

Bons estudos a todos!

Teorema de Tales

Olá pessoal!

O vídeo trata da história do teorema de Tales e suas aplicações. Assistam!

Forte abraço.

Ampliação - Razão de semelhança

Olá pessoal!

Os vídeos tratam do conceito de ampliação e do cálculo da razão de semelhança. Assistam!
Forte abraço.

Desculpas

Olá pessoal!

      Todos que acessam esse blog desde o início, sabem da seriedade do trabalho que tenho desenvolvido até então. Alguém com o objetivo de desrespeitar este ambiente, postou na caixa de "mensagens", palavras que certamente eu não diria para ninguém, nem tão pouco divulgaria no blog, pois esse espaço é o espelho do meu trabalho no mundo todo.
      Por isso peço desculpas pelo que essa "pessoa" escreveu e assinou com meu nome. Vou retirar esse ítem do blog e procurar uma maneira segura para aqueles que realmente utilizam esse espaço para a aprendizagem, possa deixar seu recado ou sua contribuição.

Um grande abraço a todos!

Joelson Lima da Silva.

Fórum: Dúvidas sobre os assuntos da recuperação 1º bimestre.

Olá pessoal!

Vamos usar esse espaço para discutir e tirar dúvidas sobre os assuntos da recuperação. Coloque aqui suas dúvidas ou responda as que você souber, para poder ajudar seu colega. Precisamos levar o estudo à sério e fazer isso em grupo, é a forma mais fácil de superar nossas dificuldades.

Clique no título desta postagem para deixar sua dúvida ou responder a dúvida de seu colega!
Bom estudo a todos!!

Revisão 8º e 9º ano para recuperação 1º bimestre

Olá pessoal!

Segue a revisão feita segunda (26 de abril de 2010) para a recuperação, 1º bimestre.

Bons estudos!

 

1ª aula presencial MEB III

Olá pessoal!

Segue a primeira aula presencial detalhada para ajudar no estudo para a primeira avaliação.
Bom estudo a todos!
Abraço.

Resolução da 2ª prova

Olá pessoal!

A 2ª prova do segundo bimestre resolvida.

Revisão Unidade 1: Números - 8º ano

Olá pessoal!

Mais um material para ajudar em seus estudos.

Programa de recuperação 1º bimestre

Olá pessoal!

Fiquem atentos ao programa da recuperação! As recuperações serão realizadas no turno oposto, entre os dias 26 e 30 de abril.

Programa de recuperação 1º bimestre – Matemática – turno manhã – 2010.



8º ano


Equação do primeiro grau


Porcentagem


Regra de três (proporcionalidade)


Unidade 1: Números


Páginas 11 até 63


9º ano


Sistema de equações do primeiro grau


Porcentagem


Regra de três (proporcionalidade)


Unidade 1: Conjuntos numéricos


Páginas 11 até 62

Estudem bastante!
Acredito no potencial de vocês!
Abraço

Revisão 8º e 9º ano para a 2ª prova

Olá pessoal!

As listas estão todas resolvidas. Agora é pegar esse material, mais o livro e o caderno, e estudar bastante. Qualquer dúvida, poste um comentário aqui no blog.
Bom Estudo para todos!

Programa da 2ª prova 1º bimestre

Programa da 2ª prova 1º bimestre – Matemática – turno manhã – 2010.



8º ano


Unidade 1: Números


Páginas 11 até 63


9º ano


Unidade 1: Conjuntos numéricos


Páginas 11 até 62


Bom Estudo!!

O que é Matemática???

O que é Matemática ?

   Realmente é muito difícil definir em poucas palavras o que é matemática e toda definição não conseguirá expressar todo o significado da matemática; porém vou tentar dar uma noção : A priori a palavra matemática deriva da palavra grega "matemathike" que significa "ensinamentos". A matemática é uma ciência formal (seus axiomas são independentes dos axiomas das outras ciências) que se baseia em : axiomas, teoremas, corolários, lemas, postulados e proposições para chegar a conclusões teóricas e práticas. Ela também pode ser vista como um sistema formal de pensamento para reconhecer, classificar e explorar padrões. Mas o que é um padrão ? Vou dar-lhes exemplos para que este conceito fique mais fácil : 1) As listas dos tigres e as manchas das hienas mostram uma certa regularidade matemática, 2)O número de pétalas das flores mostra-nos um tipo de padrão curioso, pois na grande maioria delas o número de pétalas ocorre nesta estranha sequência : 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89. Observe que 3 + 5 = 8 , 5 + 8 = 13 e assim por diante. Realmente temos que admitir que há muita beleza na natureza, para concluir isso não é necessário saber muita matemática. Porém há muita beleza também no método matemático, o qual a partir de indícios, deduzem-se regras, mas é um tipo diferente de beleza que se aplica às idéias e não às coisas.Podemos além destas duas definições dar uma mais técnica : A matemática como uma expressão da mente humana, ativará os reflexos, o contemplamento da razão e o desejo pela perfeição estética. É também chamada por muitos de linguagem universal (é uma linguagem porque é formada por signos linguísticos que passam idéias e significados). Ela pode ser dividida em matemática pura e aplicada e seus elementos básicos são a lógica e a intuição, análise e construção, generalização e individualização.

fonte: http://www.ime.usp.br/~masaki/mat.html

Outro texto interessante, veja no site: 
http://www.e-escola.pt/canal.asp?nome=matematica

O dia do número Pi

Fonte: http://revistagalileu.globo.com/Revista/Common/0,,EMI126810-17770,00-CURIOSIDADES+SOBRE+O+NUMERO+PI.html

Curiosidades sobre o número Pi

14 de março é comemorado como o dia do número pi (π) por causa dos seus famosos primeiros dígitos 3,14

por Redação Galileu

Mesmo que você não trabalhe com números e as ciências exatas não sejam suas favoritas, tem, no mínimo, uma vaga lembrança do pi. Ele é obtido pela divisão da circunferência de um círculo por seu diâmetro. O resultado é sempre a dízima 3,1415927 (e, por aí vai, ela nunca chega ao fim). A data foi estaelecida por causa dos primeiros números (3 = mês de março; 14 = dia). Para comemorar a, o site da revista NewScientist publicou fatos curiosos sobre o pi, confira alguns:


Pi no espaço

O astrônomo Robert Mattews, da Universidade de Aston na Inglaterra, combinou dados astronômicos com teoria numérica para calcular o pi. Ele usou o fato de que, para qualquer grande amostragem de números aleatórios, a probabilidade de encontrarmos números sem um fator comum é 6/pi2 . Fator comum é quando dois números tem algum divisor comum, além do número 1. Por exemplo: 3 e 7 não têm fatores comuns, 12 e 10 tem como fator comum o número 2.

Mattews calculou a distância angular entre as 100 estrelas mais brilhantes do espaço e transformou isso em 1 milhão de pares de números aleatórios. Destes, aproximadamente 61% não tinha fatores comuns. Ele chegou a um valor de 3.12772 para pi, o que é 99,6% correto.
Pi na água
A constante matemática está na rota de todos os rios curvos que deságuam no mar. A sinuosidade de um rio é descrita pelo comprimento de sua curva dividido pela distância deste ponto até o oceano em linha reta. O resultado é que, em média, os rios têm uma sinuosidade de aproximadamente 3,14 – o número pi.

Pi na literatura
No livro inédito “Alex's Adventures in Numberland” (algo como “As aventuras de Alex na Terra dos números”, o jornalista Alex Bellos fala de como o número pi inspirou uma brincadeira literária conhecida como Pilish. Ela consiste em poemas – ou “piemas” – onde o número de letras de palavras sucessivas é determinado por pi. O próprio autor já escreveu um livro de 10 mil palavras com a técnica.

Resolução da 1ª prova 2010

Olá pessoal!

Segue a resolução da primeira prova do primeiro bimestre de matemática.
Baixe e olhe o que vc acertou ou errou!
Bom estudo!!

Operações com frações

Olá pessoal, mais um material para o estudo das operações com frações.

Bons estudos!! 

Lista de revisão 1ª prova 1º bimestre

Olá pessoal!

Baixe a lista que na segunda-feira faremos em sala.
Quando vc baixar e imprimir, deixe um recado no comentário abaixo como no exemplo.

"Joelson Lima - 8º ano manhã - ok."

Clique no link abaixo para fazer o download.

Lista 8º ano

Lista 9º ano

Regra de três simples

fonte:http://www.somatematica.com.br/fundam/regra3s.php

Regra de três simples

Regra de três simples é um processo prático para resolver problemas que envolvam quatro valores dos quais conhecemos três deles. Devemos, portanto, determinar um valor a partir dos três já conhecidos.
        Passos utilizados numa regra de três simples:
        1º) Construir uma tabela, agrupando as grandezas da mesma espécie em colunas e mantendo na mesma linha as grandezas de espécies diferentes em correspondência.
        2º) Identificar se as grandezas são diretamente ou inversamente proporcionais.
        3º) Montar a proporção e resolver a equação.
        Exemplos:
        1) Com uma área  de absorção de raios solares de 1,2m², uma lancha com motor movido a energia solar consegue produzir 400 watts por hora de energia. Aumentando-se essa área para 1,5m², qual será a energia produzida?
        Solução: montando a tabela:

Área (m2)	Energia (Wh)
1,2	400
1,5	x

        Identificação do tipo de relação:

        Inicialmente colocamos uma seta para baixo na coluna que contém o x (2ª coluna).
        Observe que: Aumentando a área de absorção, a energia solar aumenta.
        Como as palavras correspondem (aumentando - aumenta), podemos afirmar que as grandezas são diretamente proporcionais. Assim sendo, colocamos uma outra seta no mesmo sentido (para baixo) na 1ª coluna. Montando a proporção e resolvendo a equação temos:

Logo, a energia produzida será de 500 watts por hora.

---

        2) Um trem, deslocando-se a uma velocidade média de 400Km/h, faz um determinado percurso em 3 horas. Em quanto tempo faria esse mesmo percurso, se a velocidade utilizada fosse de 480km/h?
        Solução: montando a tabela:

Velocidade (Km/h)	Tempo (h)
400	3
480	x

        Identificação do tipo de relação:

        Inicialmente colocamos uma seta para baixo na coluna que contém o x (2ª coluna).
        Observe que: Aumentando a velocidade, o tempo do percurso diminui.
        Como as palavras são contrárias (aumentando - diminui), podemos afirmar que as grandezas são inversamente proporcionais. Assim sendo, colocamos uma outra seta no sentido contrário (para cima) na 1ª coluna. Montando a proporção e resolvendo a equação temos:

Logo, o tempo desse percurso seria de 2,5 horas ou 2 horas e 30 minutos.

---

        3) Bianca comprou 3 camisetas e pagou R$120,00. Quanto ela pagaria se comprasse 5 camisetas do mesmo tipo e preço?
        Solução: montando a tabela:

Camisetas	Preço (R$)
3	120
5	x

        Observe que: Aumentando o número de camisetas, o preço aumenta.
        Como as palavras correspondem (aumentando - aumenta), podemos afirmar que as grandezas são diretamente proporcionais. Montando a proporção e resolvendo a equação temos:

Logo, a Bianca pagaria R$200,00 pelas 5 camisetas.

---

        4) Uma equipe de operários, trabalhando 8 horas por dia, realizou determinada obra em 20 dias. Se o número de horas de serviço for reduzido para 5 horas, em que prazo essa equipe fará o mesmo trabalho?
        Solução: montando a tabela:

Horas por dia	Prazo para término (dias)
8	20
5	x

        Observe que: Diminuindo o número de horas trabalhadas por dia, o prazo para término aumenta.
        Como as palavras são contrárias (diminuindo - aumenta), podemos afirmar que as grandezas são inversamente proporcionais. Montando a proporção e resolvendo a equação temos:

Sistemas de Equações do 1º grau com duas variáveis

fonte: http://www.somatematica.com.br/fundam/equacoes2v2.php
Sistemas de Equações
    Considere o seguinte problema:
   Pipoca, em sua última partida, acertou x arremessos de 2 pontos e y arremessos de 3 pontos. Ele acertou 25 arremessos e marcou 55 pontos. Quantos arremessos de 3 pontos ele acertou?
   Podemos traduzir essa situação através de duas equações, a saber:
                x + y = 25         (total de arremessos certo)
                2x + 3y = 55     (total de pontos obtidos)

    Essas equações contém um sistema de equações.
    Costuma-se indicar o sistema usando chave.
                           
    O par ordenado (20, 5), que torna ambas as sentenças verdadeiras, é chamado solução do sistema. Um sistema de duas equações com duas variáveis possui uma única solução.

Resolução de Sistemas

    A resolução de um sistema de duas equações com duas variáveis consiste em determinar um par ordenado que torne verdadeiras, ao mesmo tempo, essas equações.
    Estudaremos a seguir alguns métodos:

Método de substituição

    Solução

• 
  
  determinamos o valor de x na 1ª equação.

                        x = 4 - y

• Substituímos esse valor na 2ª equação.

                        2 . (4 - y) -3y = 3 

• Resolvemos a equação formada.

8 - 2y -3y = 3      8 - 2y -3y = 3                                  -5y = -5   => Multiplicamos por -1 5y = 5        y = 1

• Substituímos o valor encontrado de y, em qualquer das equações, determinando x.

x  + 1 =  4 x =  4 - 1 x = 3

• A solução do sistema é o par ordenado (3, 1).

                                V = {(3, 1)}
Método da adição
   Sendo U = , observe a solução de cada um dos sistemas a seguir, pelo método da adição.
   Resolva o sistema abaixo:

   Solução

• 
  
  Adicionamos membros a membros as equações:

                       

                           2x = 16

                           

                            x = 8

• 
  
  Substituímos o valor encontrado de x, em qualquer das equações, determinado y:

                            8 + y = 10

                            y = 10 - 8

                            y = 2

        A solução do sistema é o par ordenado (8, 2)

                            V = {(8, 2)}