Adição e Subtração de Frações
Para adicionar ou subtrair frações de mesmo denominador, somam-se os numeradores e repete-se o denominador.
Temos que analisar dois casos:
1º) denominadores iguais
Para somar frações com denominadores iguais, basta somar os numeradores e conservar o denominador.
Para subtrair frações com denominadores iguais, basta subtrair os numeradores e conservar o denominador.
Observe os exemplos:
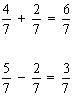
2º) denominadores diferentes
Para somar frações com denominadores diferentes, uma solução é obter frações equivalentes, de denominadores iguais ao mmc dos denominadores das frações.
Obtendo o mmc dos denominadores temos mmc (5,2) = 10.
Resumindo: utilizamos o mmc para obter as frações equivalentes e depois somamos normalmente as frações, que já terão o mesmo denominador, ou seja, utilizamos o caso 1.
Multiplicação e divisão de números fracionários
Nas multiplicações de frações multiplica-se o numerador com numerador e denominador com denominador. Se necessário, simplifique o produto.
Veja os exemplos:
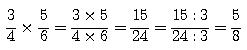
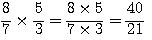
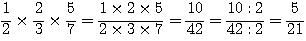
Na divisão de números fracionários, devemos multiplicar a primeira fração pelo inverso da segunda. Se necessário simplifique.
Veja o exemplo abaixo:
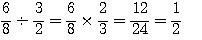
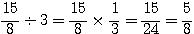
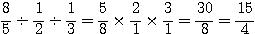
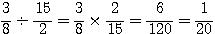
Para adicionar ou subtrair frações de mesmo denominador, somam-se os numeradores e repete-se o denominador.
Temos que analisar dois casos:
1º) denominadores iguais
Para somar frações com denominadores iguais, basta somar os numeradores e conservar o denominador.
Para subtrair frações com denominadores iguais, basta subtrair os numeradores e conservar o denominador.
Observe os exemplos:
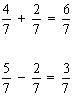
2º) denominadores diferentes
Para somar frações com denominadores diferentes, uma solução é obter frações equivalentes, de denominadores iguais ao mmc dos denominadores das frações.
| Exemplo: somar as frações |
Obtendo o mmc dos denominadores temos mmc (5,2) = 10.
(10:5). 4 = 8 | (10:2).5 = 25 | ||
Resumindo: utilizamos o mmc para obter as frações equivalentes e depois somamos normalmente as frações, que já terão o mesmo denominador, ou seja, utilizamos o caso 1.
Multiplicação e divisão de números fracionários
Nas multiplicações de frações multiplica-se o numerador com numerador e denominador com denominador. Se necessário, simplifique o produto.
Veja os exemplos:
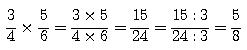
Na divisão de números fracionários, devemos multiplicar a primeira fração pelo inverso da segunda. Se necessário simplifique.
Veja o exemplo abaixo:
fonte: http://www.colegioweb.com.br/matematica-infantil/operacoes-com-fracoes





3 comentários:
Muito legal!Me ajudou bastante!
não tem nada a ver com o que eu quero,
vocês deveriam ter vergonha do conteúdo que vocês colocam no site,tirei 0,5 (cinco decimoa) na prova seguindo vocês
realmente n tem nada a ver com o q eu pedi
Postar um comentário